摘要：本文研究在分布式系统中，事件发生先后顺序的概念，并说明如何定义事件之间的偏序关系。论文给出了一种用于同步逻辑时钟系统的分布式算法，该逻辑时钟可用于确定事件的全序排序。其中，全序是描述解决同步问题的一种方法。该算法专门用于同步物理时钟，并且给出时钟同步的误差。

引入｜Introduction

The concept of time is fundamental to our way of thinking. It is derived from the more basic concept of the order in which events occur. We say that something happened at 3:15 if it occurred after our clock read 3:15 and before it read 3:16. The concept of the temporal ordering of events pervades our thinking about systems. For example, in an airline reservation system we specify that a request for a reservation should be granted if it is made before the flight is filled. However, we will see that this concept must be carefully reexamined when considering events in a distributed system.

时间的概念是我们思考的基础。而它源于事件发生顺序这一更基础的概念。当一件事情发生在时钟显示 3:15 且未到 3:16 之前，那我们就说它发生在 3:15。对事件的时间顺序概念遍布于我们对系统的思考。例如，我们在机票预定系统中发起的预定请求，如果它发生在航班订满之前，那就应该被接受。但在分布式系统中，我们会发现事件的时间顺序概念需要被重新审视。

A distributed system consists of a collection of distinct processes which are spatially separated, and which communicate with one another by exchanging messages. A network of interconnected computers, such as the ARPA net, is a distributed system. A single computer can also be viewed as a distributed system in which the central control unit, the memory units, and the input-output channels are separate processes. A system is distributed if the message transmission delay is not negligible compared to the time between events in a single process.

分布式系统由空间上彼此分开的一组独立进程组成，进程间通过交换消息进行通信。计算机互联的网络，比如 ARPANET（阿帕网）就是一个分布式系统。一台集成了 CPU、内存、I/O 通道等独立处理单元的计算机也可以被视为分布式系统。如果相对于单进程中事件之间的时间，消息传输的延时大到不可忽略时，系统就是分布式的。

We will concern ourselves primarily with systems of spatially separated computers. However, many of our remarks will apply more generally. In particular, a multiprocessing system on a single computer involves problems similar to those of a distributed system because of the unpredictable order in which certain events can occur.

本文主要关注空间分离的计算机系统。但我们的诸多观点可以得到更普遍的应用。特别的，由于不可预知的事件发生顺序，单机上多进程系统也涉及到类似分布式系统中的问题。

In a distributed system, it is sometimes impossible to say that one of two events occurred first. The relation " happened before" is therefore only a partial ordering of the events in the system. We have found that problems often arise because people are not fully aware of this fact and its implications.

在分布式系统中，有时候无法确定两个事件哪个先发生。「之前发生」（happened before）只是系统中事件之间的偏序（Partial Ordering）。我们发现，由于人们没有充分认知到这个事实和它的含义，导致问题的出现。

In this paper, we discuss the partial ordering defined by the " happened before" relation, and give a distributed algorithm for extending it to a consistent total ordering of all the events. This algorithm can provide a useful mechanism for implementing a distributed system. We illustrate its use with a simple method for solving synchronization problems. Unexpected, anomalous behavior can occur if the ordering obtained by this algorithm differs from that perceived by the user. This can be avoided by introducing real, physical clocks. We describe a simple method for synchronizing these clocks, and derive an upper bound on how far out of synchrony they can drift.

在本论文中，我们讨论由「之前发生」所定义的偏序，提供一个分布式算法来将其扩展成对所有事件一致的全序（Total Ordering）。该算法提供了实现分布式系统的有效途径。我们用解决同步问题的一个简单方法，来说明该算法的使用。然而，如果通过该算法获取的事件顺序和用户感知的不同时，会导致异常行为。这可以通过引入真实的物理时钟来规避。我们描述了一种用于同步这些时钟的简单方法，并推导了时钟同步漂移的误差上限。

偏序｜The Partial Ordering

Most people would probably say that an event a happened before an event b if a happened at an earlier time than b. They might justify this definition in terms of physical theories of time. However, if a system is to meet a specification correctly, then that specification must be given in terms of events observable within the system. If the specification is in terms of physical time, then the system must contain real clocks. Even if it does contain real clocks, there is still the problem that such clocks are not perfectly accurate and do not keep precise physical time. We will therefore define the " happened before" relation without using physical clocks.

大部分人会认为，如果事件 A 发生的时间比事件 B 发生时间早，则事件 A 是在事件 B 「之前发生」。他们根据物理时间的理论来证明该定义的正确性。然而，如果系统要正确地满足一项规约，则该规约必须根据系统可观测的事件给出。如果规约是基于物理时间，那么系统必须要包含真实的时钟。即使包含了真实时钟，仍然存在时钟非完美精确和保持精准物理时间的问题。因此我们不使用物理时钟来定义「之前发生」这一关系。

We begin by defining our system more precisely. We assume that the system is composed of a collection of processes. Each process consists of a sequence of events. Depending upon the application, the execution of a subprogram on a computer could be one event, or the execution of a single machine instruction could be one event. We are assuming that the events of a process form a sequence, where a occurs before b in this sequence if a happens before b. In other words, a single process is defined to be a set of events with an a priori total ordering. This seems to be what is generally meant by a process. It would be trivial to extend our definition to allow a process to split into distinct subprocesses, but we will not bother to do so.

我们从更精准的定义系统开始。假设系统由一组进程组成。每个进程包含了一系列事件。根据应用程序的不同，事件可以是执行子程序，或者是执行单个机器指令。我们假设一个进程中的事件组成一个序列，当a在b「之前发生」，则事件序列里a就在b之前。换个说法，进程是一组全序事件的集合。这似乎也是通常意义上进程的含义。我们也可以把上述定义扩展到子进程，但没必要这么做。

We assume that sending or receiving a message is an event in a process. We can then define the " happened before" relation, denoted by “->”, as follows.

假设发送或接受消息是进程中的事件。我们可以用符号->表示「之前发生」，如下所示：

Definition. The relation “->” on the set of events of a system is the smallest relation satisfying the following three conditions: (1) If a and b are events in the same process, and a comes before b, then a -> b. (2) If a is the sending of a message by one process and b is the receipt of the same message by another process, then a -> b. (3) If a -> b and b -> c then a -> c. Two distinct events a and b are said to be concurrent if a -/-> b and b -/-> a.

定义。系统中一组事件之间的->关系，是满足以下三个条件的最小关系：

1. 如果 a 和 b 是同一进程中的事件，且 a 在 b 之前，则 a -> b；
2. 如果 a 是一个进程的消息发送事件，b 是另一进程的消息接收事件，则 a -> b ；
3. 如果 a -> b 且 b -> c ，则 a -> c。如果两个独立事件满足 a !-> b 且 b !-> a ，则二者并行（concurrent）；

We assume that a -/-> a for any event a. (Systems in which an event can happen before itself do not seem to be physically meaningful.) This implies that -/-> is an irreflexive partial ordering on the set of all events in the system.

假设任意事件 a，a !-> a（事件在自身之前发生的系统，并不存在物理意义）。这表明->表示的是，系统中事件之间非自反性的偏序关系。

It is helpful to view this definition in terms of a “space-time diagram” such as Figure 1. The horizontal direction represents space, and the vertical direction represents time–later times being higher than earlier ones. The dots denote events, the vertical lines denote processes, and the wavy lines denote messagesfl It is easy to see that a -> b means that one can go from a to b in the diagram by moving forward in time along process and message lines. For example, we have p₁ -> r₄ in Figure 1.

结合下图 1 所示的时空图，可以帮助我们理解上述定义。其中横轴表示空间，纵轴表示时间——时间靠后则纵坐标越大。图中的点表示事件，竖向的直线表示进程，曲线表示进程间传递的消息。显而易见，a -> b 表示在进程间通过消息，从 a 到达 b。比如图 1 中有 p₁ -> r₄。

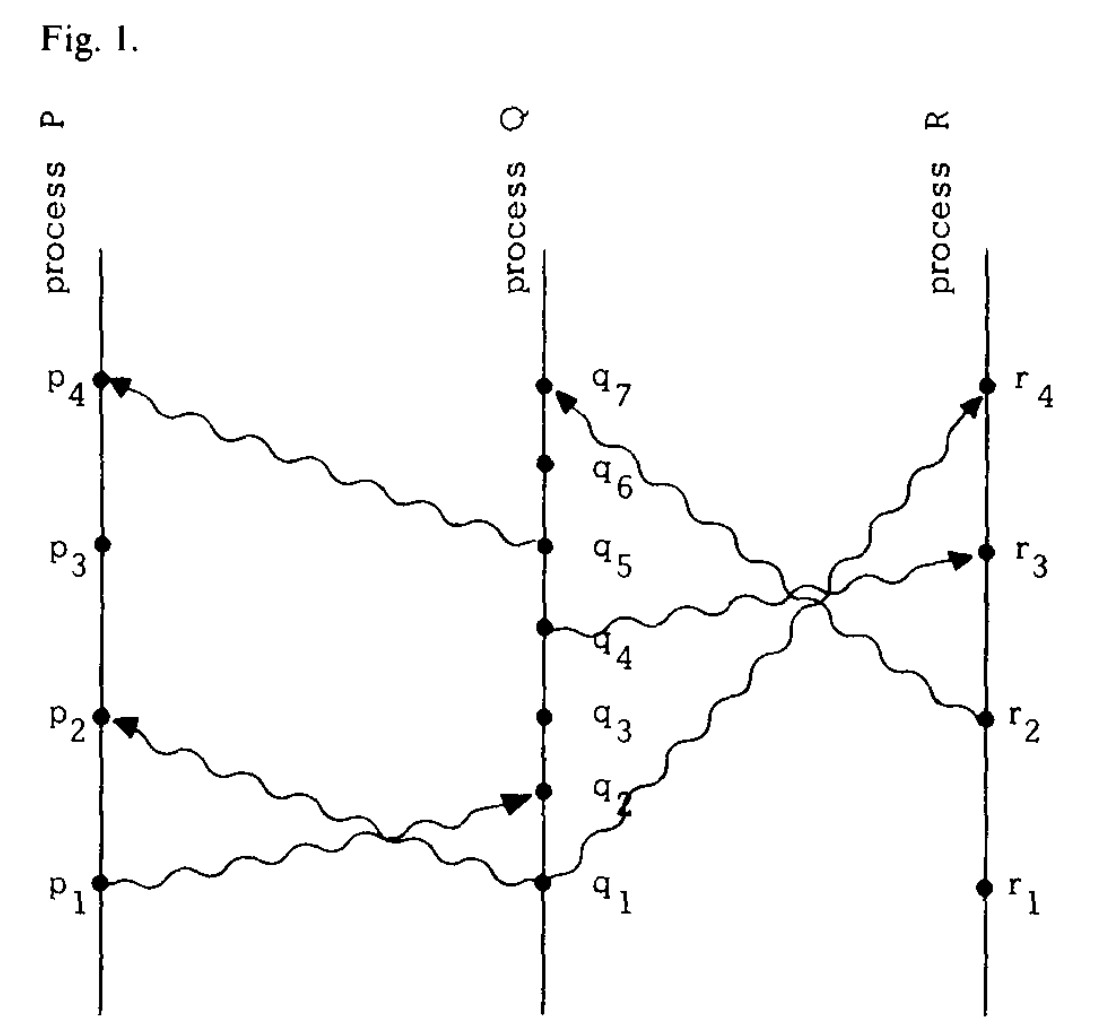
Another way of viewing the definition is to say that a -> b means that it is possible for event a to causally affect event b. Two events are concurrent if neither can causally affect the other. For example, events p₃ and q₃ of Figure 1 are concurrent. Even though we have drawn the diagram to imply that q₃ occurs at an earlier physical time than p₃, process P cannot know what process Q did at q₃ until it receives the message at p₄, (Before event p₄, P could at most know what Q was planning to do at q₃.)

对该定义的另一种理解是，a -> b 表示事件 a 有可能导致事件 b 发生。当两个事件互相不为因果时，两者就是并行的。举例来说，图 1 里的事件 p₃ 和 q₃ 是并行发生的，即使图中描述的情形是 q₃ 发生的物理时间是在在 p₃ 之前，但对进程 P 而言，在 p₄ 时间点收到消息之前，它无法得知进程 Q 在 q₃ 时在做什么。（在事件 p₄ 之前，进程 P 最多知道进程 Q 在 q₃ 时将要做什么）。

This definition will appear quite natural to the reader familiar with the invariant space-time formulation of special relativity, as described for example in [1] or the first chapter of [2]. In relativity, the ordering of events is defined in terms of messages that could be sent. However, we have taken the more pragmatic approach of only considering messages that actually are sent. We should be able to determine if a system performed correctly by knowing only those events which did occur, without knowing which events could have occurred.

这个定义对于熟悉狭义相对论不变时空方程的读者，理解起来非常自然。现实中，通过可能被发送的消息来定义事件顺序。但是我们采用更加务实的办法，即只考虑实际被发送的消息。当系统知道明确已发生的事件，我们就可以确定系统是否正确运行，而无需知道那些可能发生的事件。

逻辑时钟｜Logical Clocks

We now introduce clocks into the system. We begin with an abstract point of view in which a clock is just a way of assigning a number to an event, where the number is thought of as the time at which the event occurred. More precisely, we define a clock C_i for each process P_i to be a function which assigns a number C_i<a> to any event a in that process. The entire system ofclbcks is represented by the function C which assigns to any event b the number C<b>, where C<b> = C_j(b) if b is an event in process P_j. For now, we make no assumption about the relation of the numbers C_i<a> to physical time, so we can think of the clocks Ci as logical rather than physical clocks. They may be implemented by counters with no actual timing mechanism.

现在，我们引入时钟。从一个抽象的观点开始——时钟是为事件分配编号的方式，其中编号可看作为事件发生的时间。更精确的表述，对于任意进程 P_i，定义时钟 C_i，其中，C_i(a) 表示进程 P_i 中事件 a 的编号分配函数。整个时钟系统通过函数 C 来分配，如果事件 b 在进程 P_j 中，那么 C(b) = C_j(b)。到目前为止，我们没有做任何关于时钟 C_i(a) 和物理时间关系的假设，所以我们可以把 C_i(a) 看成是逻辑时钟而非物理时钟。逻辑时钟可以不通过真实的计时工具来进行计数。

We now consider what it means for such a system of clocks to be correct. We cannot base our definition of correctness on physical time, since that would require introducing clocks which keep physical time. Our definition must be based on the order in which events occur. The strongest reasonable condition is that if an event a occurs before another event b, then a should happen at an earlier time than b. We state this condition more formally as follows.

Clock Condition. For any events a, b:
    if a -> b then C(a) < C(b).

我们现在来思考该时钟系统正确性的含义。我们不能把定义的正确性建立在物理时钟之上，否则会导致引入记录物理时间的时钟。逻辑时钟的定义必须基于事件发生的顺序。最合理的条件是，如果事件 a 发生在事件 b 之前，那么 a 的发生事件应该比 b 更早。通过下面的式子更正式的进行表达该条件：

时钟条件，对于任意事件 a、b：
            if a -> b then C(a) < C(b)

Note that we cannot expect the converse condition to hold as well, since that would imply that any two concurrent events must occur at the same time. In Figure 1, p₂ and p₃ are both concurrent with q₃, so this would mean that they both must occur at the same time as q₃, which would contradict the Clock Condition because p₂ -> p₃.

注意，上述式子的反推是不成立的（C(a) < C(b)，不能反推出 a -> b），否则就意味着两个并行的事件必须发生在同一时间。在图 1 中，事件 p₂、p₃ 均和事件 q₃ 并行，如果要求它们必须和 q₃ 在相同时间发生，就和时钟条件 p₂ -> p₃ 相矛盾。

It is easy to see from our definition of the relation “->” that the Clock Condition is satisfied if the following two conditions hold.
 C1. If a and b are events in process P_i, and a comes before b, then C_i(a) < C_i(b).
 C2. If a is the sending of a message by process P_i and b is the receipt of that message by process P_j, then C_i(a) < C_j(b).

从对->关系的定义中，容易得出，满足时钟条件需要符合以下两点：

• C1: 当进程 P_i 中的事件 a 在事件 b 之前，则 C_i(a) < C_i(b)
• C2: 当事件 a 是进程 P_i 的消息发送事件，事件 b 是进程 P_j 的消息接收事件，则 C_i(a) < C_j(b)

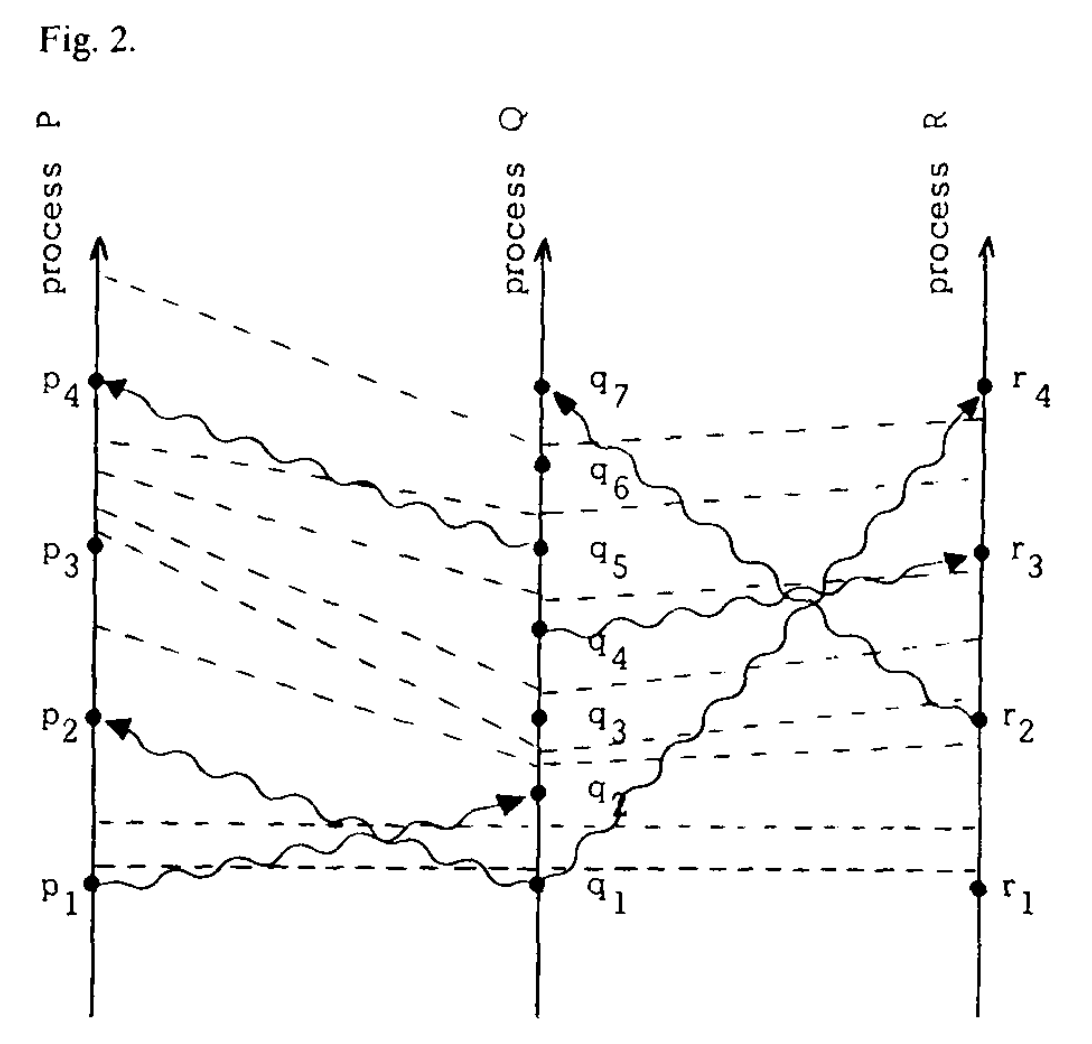
Let us consider the clocks in terms of a space-time diagram. We imagine that a process clock “ticks” through every number, with the ticks occurring between the process events. For example, if a and b are consecutive events in process P_i with C_i(a) = 4 and C_i(b) = 7, then clock ticks 5, 6, and 7 occur between the two events. We draw a dashed “tick line” through all the likenumbered ticks of the different processes. The spacetime diagram of Figure 1 might then yield the picture in Figure 2. Condition C1 means that there must be a tick line between any two events on a process line, and condition C2 means that every message line must cross a tick line. From the pictorial meaning of ->, it is easy to see why these two conditions imply the Clock Condition.

结合时间-空间图来分析时钟。我们想象一个进程的时钟会对每个数字做「滴答」，且「滴答」发生在进程中的事件之间。举个例子，如果进程 P_i 中的相邻事件 a 和 b，有 C_i(a) = 4 和 C_i(b) = 7，那么时钟会在这两个事件中间，依次滴答 5，6，7。我们把不同进程间连续的「滴答」用虚线连接，图 1 就变成如下图 2。条件 C1 意味着同一进程中任意两个事件必然存在一条「滴答」虚线；条件 C2 意味着任意消息线必然会穿过一条「滴答」线。通过对->关系的图示，很容易明白为什么满足上述两个条件 C1、C2 意味着时钟条件的成立。

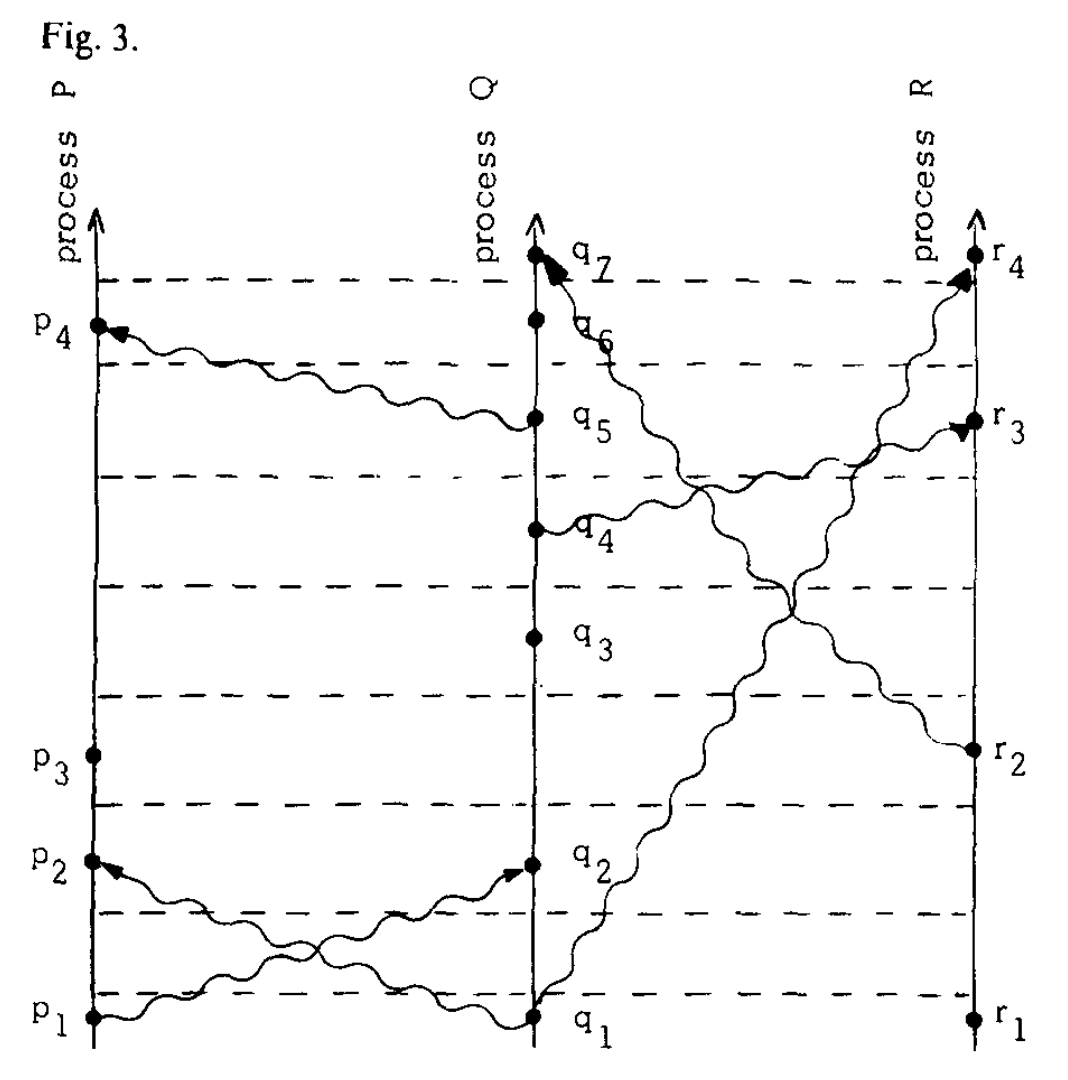
We can consider the tick lines to be the time coordinate lines of some Cartesian coordinate system on spacetime. We can redraw Figure 2 to straighten these coordinate lines, thus obtaining Figure 3. Figure 3 is a valid alternate way of representing the same system of events as Figure 2. Without introducing the concept of physical time into the system (which requires introducing physical clocks), there is no way to decide which of these pictures is a better representation.

我们可以把「滴答」线作为时间-空间笛卡尔坐标系里的时间轴。将图 2 中的「滴答」线画直，就得到如下图 3。图 3 是图 2 所表达的事件系统的另一种表现形式。如果不引入物理时间（这会导致引入物理时钟），就无法决定哪个图示更好的表现了真实系统。

The reader may find it helpful to visualize a two-dimensional spatial network of processes, which yields a three-dimensional space-time diagram. Processes and messages are still represented by lines, but tick lines become two-dimensional surfaces.

读者可能发现，如果把二维的网络进程可视化，构成一个三维的时间-空间图，会很有帮助。进程和消息仍然用线条表示，而「滴答」线则用二维平面来表示。

Let us now assume that the processes are algorithms, and the events represent certain actions during their execution. We will show how to introduce clocks into the processes which satisfy the Clock Condition. Process P_i’s clock is represented by a register C_i, so that C_i(a) is the value contained by C_i during the event a. The value of C_i will change between events, so changing C_i does not itself constitute an event.

现在假设，执行过程就是算法，事件则表示执行的具体动作。我们会展示如何在进程执行过程中，引入满足时钟条件的时钟。进程 P_i 的时钟用寄存器 C_i 表示，因此 C_i(a) 表示事件 a 发生时，寄存器 C_i 的值。C_i 的值会在事件之间变化，因此变更 C_i 的值并不构成事件本身。

To guarantee that the system of clocks satisfies the Clock Condition, we will insure that it satisfies conditions C1 and C2. Condition C1 is simple; the processes need only obey the following implementation rule:
 IR1. Each process P_i increments C_i between any two successive events.

要保证这个时钟系统可以满足时钟条件，我们要确保其同时满足条件 C1 和 C2。条件 C1 很简单，只需要进程遵循下面的规则：

• IR1. 进程 P_i 中， C_i 会在连续的事件中递增。

To meet condition C2, we require that each message m contain a timestamp T_m which equals the time at which the message was sent. Upon receiving a message timestamped T_m, a process must advance its clock to be later than T_m. More precisely, we have the following rule.
 IR2. (a) If event a is the sending of a message m by process P_i, then the message m contains a timestamp T_m = C_i(a). (b) Upon receiving a message m, process P_i sets C_i greater than or equal to its present value and greater than T_m.

要满足条件 C2，我们要求任意消息 m 包含它被发送的时间戳信息 T_m。当另一进程接收到时间戳 T_m 的消息时，该进程必须将其时钟调整到大于 T_m。我们用下面的规则做更准确的描述：

• IR2. (a) 如果事件 a 是进程 P_i 发送消息 m 的事件，而消息 m 包含了时间戳 T_m = C_i(a)。(b) 当进程 P_j 接收到消息 m 时，P_j 把 C_j 设置为大于或等于它当前的值，且大于 T_m。

In IR2(b) we consider the event which represents the receipt of the message m to occur after the setting of C_j. (This is just a notational nuisance, and is irrelevant in any actual implementation.) Obviously, IR2 insures that C2 is satisfied. Hence, the simple implementation rules IR1 and IR2 imply that the Clock Condition is satisfied, so they guarantee a correct system of logical clocks.

在规则 IR2(b) 中，我们认为接收消息 m 的事件发生在 C_j 被设置之后。很明显，规则 IR2 保证满足条件 C2。因此，规则 IR1 和 IR2 的实现，满足了时钟条件，从而保证正确的逻辑时钟系统。

全局事件顺序｜Ordering the Events Totally

We can use a system of clocks satisfying the Clock Condition to place a total ordering on the set of all system events. We simply order the events by the times at which they occur. To break ties, we use any arbitrary total ordering < of the processes. More precisely, we define a relation => as follows: if a is an event in process P_i and b is an event in process P_j, then a => b if and only if either (i) Ci(a) < Cj(b) or (ii) Ci(a) = Cj(b) and Pi < Pj. It is easy to see that this defines a total ordering, and that the Clock Condition implies that if a -> b then a => b. In other words, the relation => is a way of completing the “happened before” partial ordering to a total ordering.

我们可以用满足时钟条件的时钟系统，给系统中所有事件设置全局的顺序。简单的通过事件发生的时间进行排序。为了打破平局，我们使用了进程间的任意的一个全序关系<。更准确的说，我们定义了一种关系=>:如果 a 是进程 P_i 种的事件，b 是进程 P_j 中的事件，则当且仅当满足以下任意条件时，a => b：

• C_i(a) < C_j(b)
• C_i(a) = C_j(b) 且 P_i < P_j 。

容易发现这定义了全序（Total ordering），且时钟条件表明如果 a -> b，则 a => b。换言之，=> 关系是把「之前发生」（happened before）的偏序关系补全成全序关系的一种方式。

The ordering => depends upon the system of clocks C_i, and is not unique. Different choices of clocks which satisfy the Clock Condition yield different relations =>. Given any total ordering relation => which extends ->, there is a system of clocks satisfying the Clock Condition which yields that relation. It is only the partial ordering which is uniquely determined by the system of events.

全序关系=>依赖时钟系统 C_i，但并不唯一。选择不同的时钟，会产生不同的=>关系。给定任意一个由偏序关系->扩展而来的全序关系=>，都存在一个满足时钟条件的时钟，从而构成该关系。只有偏序关系->才是系统中的事件唯一确定的。

Being able to totally order the events can be very useful in implementing a distributed system. In fact, the reason for implementing a correct system of logical clocks is to obtain such a total ordering. We will illustrate the use of this total ordering of events by solving the following version of the mutual exclusion problem. Consider a system composed of a fixed collection of processes which share a single resource. Only one process can use the resource at a time, so the processes must synchronize themselves to avoid conflict. We wish to find an algorithm for granting the resource to a process which satisfies the following three conditions:
(I) A process which has been granted the resource must release it before it can be granted to another process.
(II) Different requests for the resource must be granted in the order in which they are made.
(III) If every process which is granted the resource eventually releases it, then every request is eventually granted.

确定事件的全序关系，对实现分布式系统非常有用。实际上，实现逻辑时钟系统的目的就是为了获取全序关系。我们会通过解决版本互斥问题来描述事件全序关系的使用。对于由一组共享单一资源的进程所组成的系统，同一时刻只能有一个进程使用该资源，因此进程间必须同步以避免冲突。我们希望找到一种满足以下 3 个条件的资源分配算法：

1. 进程要获取资源，必须要等待当前获取该资源的进程将其释放；
2. 对资源的多个请求，必须要按其创建的顺序依次处理；
3. 如果获取资源的进程最终都会释放掉资源，则所有对资源的请求都将最终成功；

We assume that the resource is initially granted to exactly one process.

我们假定单一资源初始时被授予单个进程。

These are perfectly natural requirements. They precisely specify what it means for a solution to be correct/ Observe how the conditions involve the ordering of events. Condition II says nothing about which of two concurrently issued requests should be granted first.

这都是非常自然的条件。它们准确地说明了什么样的方案才是正确的。观察上述条件是是如何关系到事件顺序的。条件-2 没有说明对并发请求资源的授予顺序。

It is important to realize that this is a nontrivial problem. Using a central scheduling process which grants requests in the order they are received will not work, unless additional assumptions are made. To see this, let P₀ be the scheduling process. Suppose P₁ sends a request to P₀ and then sends a message to P₂. Upon receiving the latter message, P₂ sends a request to P₀. It is possible for P₂’s request to reach P₀ before P₁’s request does. Condition II is then violated if P₂’s request is granted first.

意识到这是一个关键问题很重要。通过中心进程同一分配资源的方式不可取，除非设定额外的假设。来看这样一个场景，P₀ 是做资源分配的中心进程。假设进程 P₁ 向 P₀ 发送资源请求，再向 P₂ 发送一条消息。在接收到信息后，P₂向 P₀ 发送资源请求。P₂ 的请求可能会比 P₁ 先到达 P₀，如果 P₂ 的资源请求被先授予，则违背了条件-2 的要求。

To solve the problem, we implement a system of clocks with’rules IR1 and IR2, and use them to define a total ordering => of all events. This provides a total ordering of all request and release operations. With this ordering, finding a solution becomes a straightforward exercise. It just involves making sure that each process learns about all other processes' operations.

要解决该问题，我们实现了一个符合 IR1 和 IR2 的时钟系统，并且通过该时钟系统来定义所有事件的全序关系=>。这提供了所有资源请求和释放处理的全序关系。有了这个顺序，找到解决方案变得直观可行。只要确保每个进程知道所有其他进程的处理。

To simplify the problem, we make some assumptions. They are not essential, but they are introduced to avoid distracting implementation details. We assume first of all that for any two processes P_i and P_j, the messages sent from P_i to P_j are received in the same order as they are sent. Moreover, we assume that every message is eventually received. (These assumptions can be avoided by introducing message numbers and message acknowledgment protocols.) We also assume that a process can send messages directly to every other process.

为了简化问题，我们做出一些假设。它们非必需，但它们的引入可以规避过多的细节。首先假设任意两个进程 P_i 和 P_j，P_i 发送到 P_j 的多个消息，会按照它们的发送顺序依次被接收。此外，我们假设所有消息最终都会被接收（避免引入消息序号和消息确认协议）。我们还假设进程可以直接向其他任意进程发送消息。

Each process maintains its own request queue which is never seen by any other process. We assume that the request queues initially contain the single message T₀:P₀ requests resource, where P₀ is the process initially granted the resource and T₀ is less than the initial value of any clock.

每个进程维护其请求队列，并对其他进程不可见。假设请求队列初始时包含一条资源请求消息 T₀:P₀，其中 P₀ 表示初始时获得资源的进程，T₀ 小于任意时钟的初始时间。

The algorithm is then defined by the following five rules. For convenience, the actions defined by each rule are assumed to form a single event.

算法由以下 5 条规则定义。方便起见，假定每个规则定义的动作都构成一个单一事件。

1. To request the resource, process P_i sends the message T_m:P_i requests resource to every other process, and puts that message on its request queue, where T_m is the timestamp of the message.

1. 规则 1: 为了请求资源，进程 P_i 发送消息 T_m:P_i 到所有其他进程，并把该消息放进自己的请求队列里。T_m 是消息的时间戳。

2. When process P_j receives the message T_m:P_i requests resource, it places it on its request queue and sends a (timestamped) acknowledgment message to P_i

2. 规则 2: 当进程 P_j 接收到消息 T_m:P_i，将其放入到自己的请求队列，并发送一个带时间戳的 ack 消息到 P_i。

3. To release the resource, process P_i removes any T_m:P_i requests resource message from its request queue and sends a (timestamped) P_i releases resource message to every other process.

3. 规则 3: 为了释放资源，进程 P_i 移除自己所有 T_m:P_i 消息，并发送一个带时间戳的 P_i 释放资源的消息给所有其他进程。

4. When process P_j receives a P_i releases resource message, it removes any T_m:P_i requests resource message from its request queue.

4. 规则 4: 当进程 P_j 接收到 P_i 释放资源的消息，就删除自己请求队列中的所有 T_m:P_i 消息。

5. Process P_i is granted the resource when the following two conditions are satisfied: (i) There is a T_m:P_i requests resource message in its request queue which is ordered before any other request in its queue by the relation =>. (To define the relation “=>” for messages, we identify a message with the event of sending it.) (ii) P_i has received a message from every other process timestamped later than T_m.
   Note that conditions (i) and (ii) of rule 5 are tested locally by P_i.

5. 规则 5: 进程 P_i 在满足下列两个条件时，会被授予资源：i. P_i 的请求队列中有一条消息 T_m:P_i 位于队头，即=>关系。（为了定义消息的=>关系，我们会识别发送消息的事件）ii. P_i 接收到所有其他进程返回的时间戳晚于 T_m 的 ack 消息。注意，条件 i 和 ii 只需由 P_i 本地确认。

It is easy to verify that the algorithm defined by these rules satisfies conditions I-III. First of all, observe that condition (ii) of rule 5, together with the assumption that messages are received in order, guarantees that P_i has learned about all requests which preceded its current request. Since rules 3 and 4 are the only ones which delete messages from the request queue, it is then easy to see that condition I holds. Condition II follows from the fact that the total ordering => extends the partial ordering ->. Rule 2 guarantees that after Pi requests the resource, condition (ii) of rule 5 will eventually hold. Rules 3 and 4 imply that if each process which is granted the resource eventually releases it, then condition (i) of rule 5 will eventually hold, thus proving condition III.

验证由以上规则所定义的算法满足前面定义的条件 I 到条件 III 很简单。首先，观察规则 5 的条件 ii，结合对消息有序接收的前提设定，则可以保证 P_i 已经接收到所有排在它当前请求之前的请求。规则 3、4 是仅有的会删除消息的规则，所以很容易看出符合条件 I。条件 II 基于全序=>由偏序->扩展的事实而来。规则 2 保证了在 P_i 发出资源请求后，规则 5 条件 ii 最终一定会满足。规则 3 和规则 4 意味着如果进程被授予资源后最终会释放资源，则规则 5 条件 i 最终会满足，从而证明条件 III。

This is a distributed algorithm. Each process independently follows these rules, and there is no central synchronizing process or central storage. This approach can be generalized to implement any desired synchronization for such a distributed multiprocess system. The synchronization is specified in terms of a State Machine, consisting of a set C of possible commands, a set S of possible states, and a function e: C×S->S. The relation e(C, S) = S' means that executing the command C with the machine in state S causes the machine state to change to S'. In our example, the set C consists of all the commands P_i requests resource and P_i releases resource, and the state consists of a queue of waiting request commands, where the request at the head of the queue is the currently granted one. Executing a request command adds the request to the tail of the queue, and executing a release command removes a command from the queue.

这是一个分布式算法。每个进程各自遵循上述规则，且不存在中心化的同步进程或存储。该方法可以通用化的实现任何分布式系统的同步机制。同步过程是依据状态机来指定，由集合C表示可能的指令，集合S表示可能的状态，以及函数e: C * S -> S 组成。关系式e(C, S) = S'表示在状态为S时执行命令C，使状态机流转到S'。在前面的例子中，集合C包括 P_i 所有请求资源和释放资源的命令，集合S包括包括处于等待状态的请求命令队列，该队列头部是正要被授予资源的请求。执行申请资源命令会添加到队尾，而执行释放资源的命令则会从队头移除命令。

Each process independently simulates the execution of the State Machine, using the commands issued by all the processes. Synchronization is achieved because all processes order the commands according to their timestamps (using the relation =>), so each process uses the same sequence of commands. A process can execute a command timestamped T when it has learned of all commands issued by all other processes with timestamps less than or equal to T. The precise algorithm is straightforward, and we will not bother to describe it.

每个进程使用所有进程发出的命令，独立地模拟状态机的执行。之所以能够实现同步，是因为所有进程都根据其时间戳对命令进行排序（使用全序关系=>），所以每个进程使用相同的命令序列。当进程已经获悉所有其他进程发出的<= T的命令时，就可以执行带有时间戳T的命令。精确的算法已经很直观了，本文不再赘述。

This method allows one to implement any desired form of multiprocess synchronization in a distributed system. However, the resulting algorithm requires the active participation of all the processes. A process must know all the commands issued by other processes, so that the failure of a single process will make it impossible for any other process to execute State Machine commands, thereby halting the system.

这个方法可在分布式系统中实现任何形式的多进程同步。但是，该算法需要所有进程参与进来。每个进程都必须知道其他所有进程的命令，因此任意一个进程的故障都会导致其他进程无法执行状态机命令，导致系统挂起。

The problem of failure is a difficult one, and it is beyond the scope of this paper to discuss it in any detail. We will just observe that the entire concept of failure is only meaningful in the context of physical time. Without physical time, there is no way to distinguish a failed process from one which is just pausing between events. A user can tell that a system has “crashed” only because he has been waiting too long for a response. A method which works despite the failure of individual processes or communication lines is described in [3].

故障容错是一个棘手的问题，涉及它的讨论超出了本文的范围。我们只说明，故障的概念只在物理时间的语义下有意义。抛开物理时间，就无法区分进程是真的发生故障，还是处在事件之间的停止状态。用户只能通过系统长时间无响应来确认系统「挂掉了」。在进程或者通信故障时仍然能正常工作的方法，我们会在附录[3]论文中做描述。

反常行为｜Anomalous Behavior

Our resource scheduling algorithm ordered the requests according to the total ordering =>. This permits the following type of “anomalous behavior.” Consider a nationwide system of interconnected computers. Suppose a person issues a request A on a computer A, and then telephones a friend in another city to have him issue a request B on a different computer B. It is quite possible for request B to receive a lower timestamp and be ordered before request A. This can happen because the system has no way of knowing that A actually preceded B, since that precedence information is based on messages external to the system.

我们的资源调度算法根据全序关系=>对请求进行排序。这会允许以下「异常行为」：有一个全国范围计算机互联组成的系统，当一个人在计算机 A 上发送请求 A，然后电话通知另一个城市的朋友在计算机 B 上发送请求 B。对请求 B 来说，很有可能获得一个比请求 A 更小的时间戳，从而排在请求 A 前面。因为系统无法得知请求 A 实际上先于请求 B，因为「A 先于 B」是基于系统之外的消息的（上面例子中的电话）。

Let us examine the source of the problem more closely. Let ∮ be the set of all system events. Let us introduce a set of events which contains the events in ∮ together with all other relevant external events, such as the phone calls in our example. Let -> denote the “happened before” relation for ∮. In our example, we had A->B, but A-/->B. It is obvious that no algorithm based entirely upon events in ∮, and which does not relate those events in any way with the other events in ∮, can guarantee that request A is ordered before request B.

让我们更深入的探究下这个问题的根源。用符号 ∮ 表示所有系统事件的集合。我们引入一个包含 ∮ 中的事件，以及所有其他相关的外部事件的集合 ∮，比如上面例子中的电话事件。用符号->表示 ∮ 事件中「在之前发生」的关系。在我们给出的例子中，有 A->B，但 A-/->B。很明显，一个完全基于 ∮ 集合事件，而没有兼顾到 ∮ 集合事件的算法，是无法保证请求 A 排在请求 B 前面的。

There are two possible ways to avoid such anomalous behavior. The first way is to explicitly introduce into the system the necessary information about the ordering ->. In our example, the person issuing request A could receive the timestamp TA of that request from the system. When issuing request B, his friend could specify that B be given a timestamp later than TA. This gives the user the responsibility for avoiding anomalous behavior.

有两种可能的方式来规避这种异常行为。第一种是显式的引入 -> 关系。在我们的例子中，发出请求 A 的人，会获取到该请求在系统中的时间戳 TA，当发出请求 B 时，他的朋友可以让系统给 B 指定一个晚于 TA 的时间戳。这种方式让用户自己去负责避免异常行为。

The second approach is to construct a system of clocks which satisfies the following condition.
Strong Clock Condition. For any events a, b in ∮:
if a -> b then C(a) < C(b).

第二种方式是构造一个满足 Strong Clock Condition 的时钟系统：对 ∮ 集合中的任意事件 a 和 b，如果有 a->b，则必有 C(a) < C(b)。

This is stronger than the ordinary Clock Condition because -> is a stronger relation than ->. It is not in general satisfied by our logical clocks.

这比普通的 Clock Condition 更强，因为 -> 是比 -> 更强的关系。我们的逻辑时钟通常无法满足 Strong Clock Condition。

Let us identify ∮ with some set of “real” events in physical space-time, and let -> be the partial ordering of events defined by special relativity. One of the mysteries of the universe is that it is possible to construct a system of physical clocks which, running quite independently of one another, will satisfy the Strong Clock Condition. We can therefore use physical clocks to eliminate anomalous behavior. We now turn our attention to such clocks.

我们用符号 ∮ 表示物理时空中「真实」事件的集合，符号 -> 表示狭义相对论（Special Relativity）所定义的事件偏序关系。宇宙的奥秘之一是，我们有可能构造出由多个彼此独立运行的物理时钟的系统，满足 Strong Clock Condition。因此我们可以用物理时钟来消除异常行为。现在，我们把注意力转移到此类时钟上。

物理时钟｜Physical Clocks

Let us introduce a physical time coordinate into our space-time picture, and let Ci(t) denote the reading of the clock Ci at physical time t. For mathematical convenience, we assume that the clocks run continuously rather than in discrete " ticks." (A discrete clock can be thought of as a continuous one in which there is an error of up to ½ " tick" in reading it.) More precisely, we assume that Ci(t) is a continuous, differentiable function of t except for isolated jump discontinuities where the clock is reset. Then dCg(t)/dt represents the rate at which the clock is running at time t.

把物理时间坐标引入到时空图中，用Ci(t)表示在物理时间 t 时刻，读取到的时钟 Ci 的值。为了便于数学描述，我们假定时钟运动是连续的非离散的。更准确的说，我们假定Ci(t)是在时间 t 上连续可微的函数，除了在时钟被重置时产生阶跃的时间点。因此，导数dCg(t)/dt表示时钟在时间 t 时刻的运行速率。

In order for the clock Ci to be a true physical clock, it must run at approximately the correct rate. That is, we must have dCi(t)/dt ≈ 1 for all t. More precisely, we will assume that the following condition is satisfied:

为了使时钟 Ci 成为真正的物理时钟，它必须以近似正确的速率运行。 即，对所有时刻 t，都有 dCi(t)/dt≈1。更准确的说，我们假设满足下述条件：

PCI. There exists a constant k « 1
such that for all i: |dCi(t)/dt - 1| < k.
For typical crystal controlled clocks, k ≤ 10^-6

PC1. 存在常数 k « 1，对任意时钟 Ci，有：|dCi(t)/dt - 1| < k。对典型的石英钟表而言，k ≤ 10^-6

It is not enough for the clocks individually to run at approximately the correct rate. They must be synchronized so that Ci(t) ≈ Cj(t) for all i,j, and t. More precisely, there must be a sufficiently small constant ε so that the following condition holds:

时钟只是近似正确的速率运行是不够的，时钟之间必须是同步的，从而使得任意时刻 t 下的任意两个时钟 Ci 和 Cj，都满足 Ci(t) ≈ Cj(t)。更准确的说，必须有一个足够小的常数 ε，满足以下条件：

PC2. For all i, j: |Ci(t) - Cj(t)| < ε.

PC2. 对于所有的 i, j，有：|Ci(t) - Cj(t)| < ε.

If we consider vertical distance in Figure 2 to represent physical time, then PC2 states that the variation in height of a single tick line is less than ε.

如果我们用图-2中的垂直距离表示物理时间，则条件 PC2 意味着单个滴答线上的高度差小于 ε。

Since two different clocks will never run at exactly the same rate, they will tend to drift further and further apart. We must therefore devise an algorithm to insure that PC2 always holds. First, however, let us examine how small k and ε must be to prevent anomalous behavior. We must insure that the system ∮ of relevant physical events satisfies the Strong Clock Condition. We assume that our clocks satisfy the ordinary Clock Condition, so we need only require that the Strong Clock Condition holds when a and b are events in ∮ with a -/-> b. Hence, we need only consider events occurring in different processes.

由于两个不同的时钟永远不会以相同速率运行，所以时钟之间的偏差会越来越大。我们必须要设计出算法来保证条件 PC2 始终满足。但第一步，我们先探究多小的 k 和 ε 才能避免异常行为的发生。我们必须要保证 ∮ 集合中所有事件都满足 Strong Clock Condition。假定时钟满足普通的 Clock Condition，则只要让 ∮ 集合中 a -/-> b 的事件满足 Strong Clock Condition。所以我们只需要考虑发生在不同进程下的事件。

Let µ be a number such that if event a occurs at physical time t and event b in another process satisfies a -> b, then b occurs later than physical time t + µ. In other words, µ is less than the shortest transmission time for interprocess messages. We can always choose µ equal to the shortest distance between processes divided by the speed of light. However, depending upon how messages in ∮ are transmitted, µ could be significantly larger.

发生在物理时间 t 的事件 a，和另一进程中的事件 b 满足 a -> b，则 b 发生在物理时间 t + µ 之后。换言之，µ 小于进程间消息传输的最短时间。可以用进程间距离除以光速作为 µ 的值。但 µ 取决于 ∮ 中消息传输的速度，µ 可以大的多。

To avoid anomalous behavior, we must make sure that for any i, j, and t: Ci(t + µ) - Cj(t) > 0. Combining this with PC I and 2 allows us to relate the required smallness of k and ε to the value of µ as follows. We assume that when a clock is reset, it is always set forward and never back. (Setting it back could cause C1 to be violated.) PCI then implies that Ci(t + µ) - Cj(t) > (1 - k)µ. Using PC2, it is then easy to deduce that Ci(t + µ) - Cj(t) > 0 if the following inequality holds:
ε / (1 - k) ≤ µ

为了避免异常行为，必须保证对任意 i，j 和 t，有：Ci(t + µ) - Cj(t) > 0。结合条件 PC1 和 PC2，可以对所需的足够小的常数 k，ε 和 µ 进行关联。假定当时钟重置时，它只会往前而不会往后拨（往后拨会导致违反条件 C1）。那么条件 PC1 表明了 Ci(t + µ) - Cj(t) > (1 - k)·µ。利用条件 PC2，很容易得到当不等式 ε / (1 - k) ≤ µ 成立时，Ci(t + µ) - Cj(t) > 0。

This inequality together with PC 1 and PC2 implies that anomalous behavior is impossible.

该不等式成立，再结合条件 PC1 和 PC2，表明异常行为不会发生。

We now describe our algorithm for insuring that PC2 holds. Let m be a message which is sent at physical time t and received at time t'. We define v_m = t - t' to be the total delay of the message m. This delay will, of course, not be known to the process which receives m. However, we assume that the receiving process knows some minimum delay µ_m ≥ 0 such that µ_m ≤ v_m. We call Σ_m = v_m - µ_m the unpredictable delay of the message.

现在来描述保证条件 PC2 成立的算法。用 m 表示一个在物理时间 t 发送，t' 被接收的消息。定义 v_m = t - t' 来表示消息 m 总时延。这个时延当然不会被消息接收进程所获知。但我们假设接收进程知道某个最小时延 µ_m ≥ 0，且 µ_m ≤ v_m。我们称 Σ_m = v_m - µ_m 为消息 m 不可预测的时延。

We now specialize rules IRI and 2 for our physical clocks as follows:
IR 1'. For each i, if P_i does not receive a message at physical time t, then C_i is differentiable at t and dCi(t)/dt > 0.
IR2'. (a) If P_i sends a message m at physical time t, then m contains a timestamp T_m= C_i(t). (b) Upon receiving a message m at time t', process P_j sets C_i(t') equal to maximum (C_j(t' - 0), T_m + µ_m).

我们对前面的规则 IR1 和 IR2，做针对物理时钟的修改：

• IR1'. 对于任意 i，如果进程 P_i在物理时间 t 没有接收到消息，那么 C_i 在时间 t 这点可导，且 dC_i(t)/dt > 0；
• IR2'. (a) 如果 P_i 在物理时间 t 发送消息 m，则 m 包含时间戳 T_m= C_i(t)。(b) 当在物理时间 t' 接收到消息，进程 P_j 设置 C_i(t') = maximum (C_j(t' - 0), T_m + µ_m)

Although the rules are formally specified in terms of the physical time parameter, a process only needs to know its own clock reading and the timestamps of messages it receives. For mathematical convenience, we are assuming that each event occurs at a precise instant of physical time, and different events in the same process occur at different times. These rules are then specializations of rules IR1 and IR2, so our system of clocks satisfies the Clock Condition. The fact that real events have a finite duration causes no difficulty in implementing the algorithm. The only real concern in the implementation is making sure that the discrete clock ticks are frequent enough so C1 is maintained.

尽管规则是用物理时间参数描述的，但进程只需要知道它自己的时钟值，和它所接收到消息的时间戳。为了便于数学描述，我们假设每个事件都发生在精确的物理时间上，且统一进程中不同事件发生在不同时间。这些规则是对规则 IR1 和 IR2 特殊化，因此我们的时钟系统满足 Clock Condition。而真实事件会持续一段有限时间，使得算法不难实现。唯一需要注意的是，要保证时钟离散的滴答运动足够高频，使得满足 C1。

We now show that this clock synchronizing algorithm can be used to satisfy condition PC2. We assume that the system of processes is described by a directed graph in which an arc from process P_i to process P_j represents a communication line over which messages are sent directly from P_i to P_j. We say that a message is sent over this arc every τ seconds if for any t, P_i sends at least one message to P_j between physical times t and t + τ. The diameter of the directed graph is the smallest number d such that for any pair of distinct processes P_j, P_k, there is a path from P_j to P_k having at most d arcs.

现在我们来说明时钟同步算法如何保证条件 PC2。假设系统用有向图表示，其连接中进程 P_i 到 P_j 的边表示消息通信路径。每隔 τ 秒会在该边上传输，则对于任意时间 t，在物理时间 t 和 t + τ 之间，P_i 到 P_j 至少发送了一条消息。有向图的直径是满足以下条件的最小值 d：对于任意两个进程 P_j 和 P_k，连接两者的路径最多包含 d 条边。

In addition to establishing PC2, the following theorem bounds the length of time it can take the clocks to become synchronized when the system is first started.

除了建立 PC2，下面的定理限制了系统首次启动时,时钟同步所需的时长。

THEOREM. Assume a strongly connected graph of processes with diameter d which always obeys rules IR1' and IR2'. Assume that for any message m, µ_m ≤ µ for some constant µ, and that for all t > t₀: (a) PC1 holds. (b) There are constants τ and ε such that every τ seconds a message with an unpredictable delay less than ε is sent over every arc. Then PC2 is satisfied with ε ≈ d(2kτ + ε) for all t >≈ t₀ + τd, where the approximations assume µ + ε « τ.

定理 假设一个半径为 d 的由多个进程组成的强连通图始终满足规则IR1' 和 IR2'。对于任意消息 m，Um ≤ 某常数 µ，且任意时刻 t ≥ t₀，有：(a) PC1成立；(b) 存在常数 τ 和 ε，每 τ 秒都会有一个消息在不可预测的延迟部分小于 ε 的情况下在每条边上传送。则 PC2 满足，同时对于所有的t >≈ t₀ + τd，e ≈ d(2kτ + ε)，这里假设 U + ε « τ。

The proof of this theorem is surprisingly difficult, and is given in the Appendix. There has been a great deal of work done on the problem of synchronizing physical clocks. We refer the reader to [4] for an introduction to the subject. The methods described in the literature are useful for estimating the message delays µ_m and for adjusting the clock frequencies dC_{i/dt (for clocks which permit such an adjustment). However, the requirement that clocks are never set backwards seems to distinguish our situation from ones previously studied, and we believe this theorem to be a new result.}

证明上述定理非常困难，可参考附录。对于物理时钟同步问题，已经做了大量工作。建议读者阅读 [4] 了解下这个问题。文档中所描述的方法，可以用来估算消息传输时延 µ_m 以及调整时钟频率 dC_i/dt（适用于允许调整的时钟）。但是时钟不能回拨的要求，似乎使我们的场景与之前研究的那些有所不同，我们相信该定理是一个全新的结论。

结论

We have seen that the concept of “happening before” defines an invariant partial ordering of the events in a distributed multiprocess system. We described an algorithm for extending that partial ordering to a somewhat arbitrary total ordering, and showed how this total ordering can be used to solve a simple synchronization problem. A future paper will show how this approach can be extended to solve any synchronization problem.

「happening before」的概念定义了分布式系统中事件的偏序关系。我们描述了一个可以将偏序关系扩展为某种程度上的全序关系的算法，并说明了该算法如何解决简单的同步问题。未来，我们会在一篇论文中阐述如何对这种方法进行扩展以用来解决任意的同步问题。

The total ordering defined by the algorithm is somewhat arbitrary. It can produce anomalous behavior if it disagrees with the ordering perceived by the system’s users. This can be prevented by the use of properly synchronized physical clocks. Our theorem showed how closely the clocks can be synchronized.

该算法定义的全序关系有些随意。如果它与系统用户所感知的顺序不一致，则可能会导致异常行为。该问题可以通过使用正确同步的物理时钟来避免。我们的定理还展示了时钟同步可以做到多精准。

In a distributed system, it is important to realize that the order in which events occur is only a partial ordering. We believe that this idea is useful in understanding any multiprocess system. It should help one to understand the basic problems of multiprocessing independently of the mechanisms used to solve them.

在分布式系统中，认识到事件的发生顺序只是一个偏序关系是非常重要的。我们认为这个认知对于理解所有多进程系统非常有用。它有助于理解多进程处理的基本问题，抛开用来解决这些基本问题的机制。

附录

引用

• [1] Schwartz, J.T. Relativity in lllustrations. New York U. Press, New York, 1962.
• [2] Taylor, E.F., and Wheeler, J.A. Space-Time Physics, W.H. Freeman, San Francisco, 1966.
• [3] Lamport, L. The implementation of reliable distributed multiprocess systems. To appear in Computer Networks.
• [4] Ellingson, C, and Kulpinski, R.J. Dissemination of system-time. 1EEE Trans. Comm. Com-23, 5 (May 1973), 605-624.

Lamport 论文链接