Algorithms + Data Structures = Programs —— Niklaus Wirth
先搬出写了 Pascal、又拿了图灵奖的大师的名言,这里不讨论该断言的合理性,只作为本文的引子。在数据库领域,究其原理,绕不开数据存储。本文从几个经典应用出发,管窥数据结构在存储中所起到的作用。
引入
通常,像电商交易、支付系统的后端服务,往往是 I/O 密集型,I/O 性能会制约整个服务的性能。因此后端工程师往往会非常关注数据库的读写 TPS,IOPS 等监控指标。在特定的技术环节,比如为数据库表设计索引,用 Kafka 为秒杀场景提供大并发写的吞吐,这些大家非常熟悉的技术,其实都包含了对数据结构的运用。
磁盘 I/O
对数据库的读写本质是磁盘 I/O(不考虑 Redis 等内存数据库)。在讲存储中的数据结构之前,先简单介绍磁盘 I/O 特性对数据库设计的影响,详细的解释可以阅读美团技术博客 《磁盘 I/O 那些事》[1]。
传统意义上数据库需要将数据以文件的形式存储到磁盘上,对数据库的操作可以简单抽象为对磁盘文件的读写,而磁盘 I/O 耗时会影响数据库的读写性能。一次磁盘 I/O 可以拆分为:磁头寻道时间 seek time、扇区旋转延迟时间 latency time、数据传输时间 transmission time,参考下图示意。
- 磁头寻道:磁头移动到数据所在磁道位置,参考值 3-15ms;
- 扇区旋转:通过盘片的旋转,将数据所在扇区移动到磁头下方,参考值 2-5ms;
- 数据传输:数据通过系统总线从磁盘加载到内存的时间,通常小于 1ms;
寻道时间 > 旋转延迟 >> 数据传输,所以磁盘 I/O 耗时 ≈ seek time + latency time,IOPS = 1000 / (seek time + latency time)。
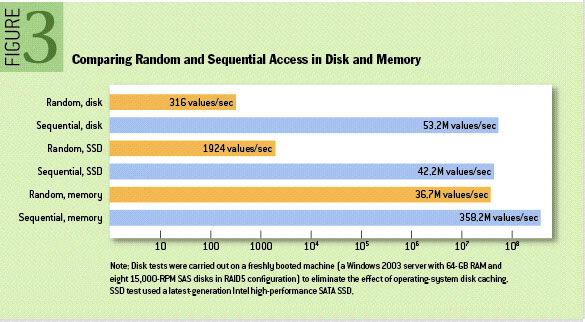
我们已经知道,磁盘的顺序 I/O 比随机 I/O 更快(参考下图),原因在于顺序 I/O 磁头几乎不用换道,或者换道的时间很短;而随机 I/O 磁头则会频繁换道。对随机 I/O 而言,7200 转的磁盘,随机 I/O 的 IOPS 通常为 70 ~ 80。而对顺序 I/O,比如读取一块连续存储的文件,理想的情况是在一次 I/O 后就可以顺序读写,其 IOPS 会非常高。因此包括数据库在内,但凡涉及存储,都会考虑更多利用顺序 I/O 来提高性能。
相对于读,写的性能瓶颈会更凸显,因此对存储的设计会优先考虑提升写性能。由于文件系统保证了文件是顺序写入,所以可以采用追加写入文件的方式实现顺序写。由于是对文件的增量追加写入,所以在数据读取时,需要倒过来检索,从最新的文件逐个往回查,比如通过简单的二分,二叉搜索树等算法进一步优化,减少 I/O 次数,归根结底性能优化还是索引。
索引
假如我们要从零开始设计一个数据库系统,实现最基础的数据写入/读取功能,直接的思路就是把数据逐行写入到磁盘上的文件中,并通过对应的 key-value 的形式映射到数据行,例如简单的 csv 文件。但数据库的设计目标不光是存储数据,还要快速找到先前存储的数据,这就带来了问题,因为从文件中逐行检索的时间复杂度是 O(n),在大数据量的情况下几乎是不可用的。
索引应运而生。如果只是为了最优化检索的时间复杂度,我们可以使用哈希实现 O(1) 的检索。但前提是哈希表存储在内存中,这在大数据量的情况下难以实现。
- 如果哈希表存储在磁盘上,会由于大量磁盘随机 I/O 导致性能不足;
- 另外哈希表索引在范围查询时,需要对区间内所有键逐个检索,效率低下。
因此大多数数据库系统并没有采用哈希表做索引,以 MySQL 为典型的 RDBMS 使用的是大家比较熟悉的 B-Tre`(各类变体均以 B-Tree 统称)。
合理地设计索引的数据结构,可以减少检索的数据量,将随机 I/O 优化为顺序 I/O,从而提升数据库的查询性能。实际上,数据库索引本身就是数据结构(参考 MySQL 对索引的定义)。
B-Tree
结合前文的分析,索引存储在磁盘上需要拥有良好的性能,并且尽可能连续,减少磁盘 I/O,比较容易想到通过有序的数据结构来实现,比如下面的二叉搜索树——
12 +-------------------------------+
/ \ | 12 | 5 | 30 | 3 | 8 | 23 | 99 |
5 30 +-------------------------------+
/ \ / \
3 8 23 99
BST 可以提供 O(logN) 时间复杂度的检索,但由于 BST 的度 <= 2,导致整个树的高度会比较大(想象成一棵瘦高树),最差情况下退化为链表,检索到目标节点所需的对比次数就越多,耗时相应增加,所以并没有实际应用在数据库系统中。得到广泛应用的是另一棵树——B-Tree(想象成一棵矮胖树)。
B-Tree 结构
B-Tree 是一种 Self-balancing Tree,它用来存储有序的数据,支持快速检索,顺序访问。B-Tree 脱胎于 BST,但是 B-Tree 度可以大于 2。其结构参考下图——
+-------------------------------+
| 7 | 16 | 30 | 3 | 8 | 23 | 99 |
+-------------------------------+
/ \________ \
/ | \
+---------------+ +--------+ +---------+
| 1 | 2 | 5 | 6 | | 9 | 12 | | 25 | 31 |
+---------------+ +--------+ +---------+
|
|
+---------+
| 10 | 11 |
+---------+
其中,B-Tree 和变体 B+ Tree 在树节点的设计上有所差异:
- B-Tree 所有节点(内节点 + 叶节点)都存储 data;而 B+ Tree 只有叶节点存储 data,内节点只存储 key;
- B+ Tree 的叶节点额外设计了一个指针,指向下一个相邻叶节点;
B-Tree 的插入、更新、删除操作会变更树的结构,从而使树保持平衡。
- B-Tree 更新已有 data, 先检索到 key,再更改 data, 写回到磁盘;
- B-Tree 添加新键,先定位到包含对应 key 的区间,将其插入到对应父节点下。如果节点所在的页已满,则需要将当前页裂变为两个半满的页,同时更新父节点以包含裂变后的页(父节点如果也满,则也进行裂变)。插入-裂变的过程示意参考下图;
- B-Tree 删除键,涉及的情况比较多,包括删叶子节点,删内节点,节点内 key 的数量,相对比较复杂;
+---------------------------+
| 10 | 20 | 30 | free space |
+---------------------------+
|
+------------------------+
| 21 | 23 | 25 | 27 | 29 |
+------------------------+
插入 24,裂变:
+--------------------------------+
| 10 | 20 | 25 | 30 | free space |
+--------------------------------+
| |
/------+ +---\
+--------------+ +--------------+
| 21 | 23 | 24 | | 25 | 27 | 29 |
+--------------+ +--------------+
B-Tree 的上述操作都是基于树的遍历,因此都是 O(logN) 的时间复杂度。另外,没有改变任意节点的深度,因此 B-Tree 始终能保持平衡,这也是它 Self-balancing 的原因。
B-Tree 性能
B-Tree 检索的本质是遍历,假设树的高度为 h,B-Tree 检索到目标数据最多需要 h-1 次 I/O,这是因为一次磁盘 I/O 加载一个节点。所以树高 h 决定了检索的效率。来看一次完整的检索过程:
- 读取根节点,对根节点内的键做二分查找,找到正确范围的子节点;
- 对子节点继续做二分查找;
- 找到目标键值;
因为二分查找的过程全内存处理,不涉及磁盘 I/O,耗时可以忽略。所以检索耗时约等于 B-Tree 目标节点深度 * 磁盘 I/O 耗时。因此 h 越小,B-Tree 的检索性能越高。这也解释了为什么 B+ Tree 比 B-Tree 更适合作为磁盘存储的索引:因为 B+ Tree 内节点不存储 data,使得内节点的度 d 比 B-Tree 大,进一步降低树高 h,减少检索过程中的磁盘 I/O 数。相关计算参考如下,其中 N 为树的节点数量——
d = page_size / (key_size + data_size + ptr_size)
h = lg(N) / lg(d)
在具体应用中,B-Tree 的根节点和高层的部分内节点会做缓存的优化,实际检索性能会比上述计算结果要好。
B-Tree 的不足
B-Tree 索引提高了数据读取效率,但也带来了负面影响:在写操作频繁的场景下,B-Tree 需要处理大量更新,变更树的结构,这导致大量的随机 I/O。因此 B-Tree 的瓶颈在于写,MySQL 对此做了优化,引入 WAL(Write-ahead Logging) 和组提交(5.6+) 。
- WAL:即在事务提交前预写日志,将事务的变更记录在日志中,而不是立即写入 B-Tree 和数据。这使得原来的随机 I/O 替换为日志文件的顺序 I/O。再批量将内存中的脏页 flush 到磁盘。
- 组提交:将写 WAL 的动作,从每次提交都要 flush,优化为多个提交合并为一次 flush。
但这部分优化并没有解决内存脏页 flush 到磁盘时,磁盘数据页物理不连续的问题。这个过程中的随机 I/O,在大写入量的情况下依然会导致性能问题。
那对于高并发写的场景,有没有其它适用的数据结构可以优化写问题?解决思路就是找到一种方式能够将磁盘 flush 过程中的随机 I/O 转换为顺序 I/O,从而提升数据库并发写的吞吐能力。为此,计算机的大牛们就设计出了 LSM Tree。
LSM Tree
LSM Tree(Log-structured Merge Tree)[3] 严格意义上并不是单一的一棵树,而是包括内存 + 磁盘,融合多种数据结构的复合结构。具体实现包括写在内存中的 MemTable,写在磁盘中的 SSTable,以及做进一步性能优化的其他数据结构。
Log-structured 是指以写日志文件的方式,增量写入磁盘,通过顺序 I/O 提升写性能;Merge 是指数据刷盘后进行数据合并,减少数据集合,精简存储空间。
这是和 B-Tree 差异的地方:B-Tree 原地更新数据,即数据只留存最新的一份,对于查询而言可以快速命中,但物理不连续的页写入带来的随机 I/O 导致写性能存在瓶颈;而 LSM Tree 增量更新数据,通过追加日志的方式将随机 I/O 转换为顺序 I/O,但数据存在多个版本,查询时需要倒序检索多个层级的文件。
简言之,LSM Tree 面向写优化,B-Tree 面向读优化。LSM Tree 通过牺牲部分读性能,换取写性能的提升。
LSM Tree 基本原理
LSM Tree 存储的数据包括两个或多个树形的组件,下图所示为最简的两组件示意图。
- 位于内存的小体积的树,为 c0 tree
- 位于磁盘的大体积的树,为 c1 tree ~ ck tree;
LSM Tree 具有以下特点:
- 每一层级的树都按 key 排序;
- 层级越低,体积越小,所存储的数据越新;
- ck-1 tree 是 ck tree 的增量数据,检索过程为低层树到高层树;
LSM Tree 的写入过程如下,参考下方示意图:
- 顺序写入 WAL,这步虽然不涉及 LSM Tree,但它防止因内存掉电而丢失数据;
- 索引写入到内存中的 c0 tree;
- 从 c0 tree 开始,数据不断被渐次 merge 到磁盘中更高层级的树(这个操作也是顺序写入);
- 高层级树在 merge 过程中,覆盖旧版本数据,删掉冗余文件,释放存储空间;
在 Google Bigtable 论文中,给出的 c0 tree 和 c1 tree 具体实现是 MemTable 和 SSTable,分别作为内存中可变数据写入、磁盘中不可变文件持久化的载体。其运转的模型如下图所示,业界主流的开源方案大都基于此实现。
MemTable
处理数据写入时,先把备份写入 WAL,再将数据插入到内存中的 MemTable,并按 key 排序。同时 MemTable 提供数据的查询。当 MemTable 写入达到一定阈值后,系统会将其转变为 Immutable MemTable,只读不可写,再 flush 到磁盘上,生成一个不可修改的新文件。同时在内存中创建新的 MemTable 记录后续的写入。内存中设计这两种 MemTable 本质是通过空间换时间,使得 MemTable flush 到磁盘的过程中不阻塞新数据的写入。
SSTable
SSTable(Sorted String Table) 是 MemTable 从内存 flush 到磁盘上的文件。SSTable 一旦创建就不再更新,即静态文件,后续的更新只会存储在新的 SSTable 中,重复和删除的记录会在新的 SSTable 中覆盖。SSTable 的存储结构如下图所示:
随着内存中的 MemTable 不断被 flush 到磁盘,SSTable 文件数量会逐渐增多,且 update 请求多的话,SSTable 间会产生相当比例的交集冗余数据。因此 LSM Tree 会对 SSTable 进行 merge 操作,移除重复、已删除的记录,减少文件数量。Merge 操作的目的,一方面是减少冗余、释放磁盘空间;另一方面,优化数据读取的效率。
LSM Tree 中写入数据流的整个过程为 MemTable -> Immutable MemTable -> SSTable,是增量写入到存量刷盘的过程。因此,LSM Tree 处理读请求时,也是按这个流程依次检索。首先检查内存中的 MemTable 和 Immutable MemTable,不存在时转到磁盘逆序检索 SSTable。因为 SSTable 有序,可以实现 O(logN) 的查找,但整体检索效率和 SSTable 数量相关,SSTable 越少,查询效率越高。
SSTable 的读性能可以在上述基础上进一步优化,比如结合布隆过滤器,提前过滤掉不存在的 key,避免不必要的全量文件读取。
SSTable 归并算法
前面提到了随着 SSTable 的堆积,将其合并是平衡 LSM Tree 读写性能的关键。原始的 LSM Tree 在对磁盘上的 SSTable 做 merge 操作时是基于 size-based 的策略,比如 HBase 采用这个算法;另一种算法是基于 level-based 策略,LevelDB、RocksDB 则选用了该算法。
size-based 顾名思义是基于 SSTable 文件大小进行分层。每层都是最多 N 个 SSTable 的集合,因为最上层的 SSTable 是由 MemTable 写入到一定阈值后持久化生成,因此同一层的 SSTable 大小可以认为相同。当某一层的 SSTable 满时,将该层的 SSTable 合并为下一层的新 SSTable。由此可以推得,相邻层的体积比为 N。这个过程就是不断的创建数量更少、体积更大的 SSTable。下图形象地展示了该过程——
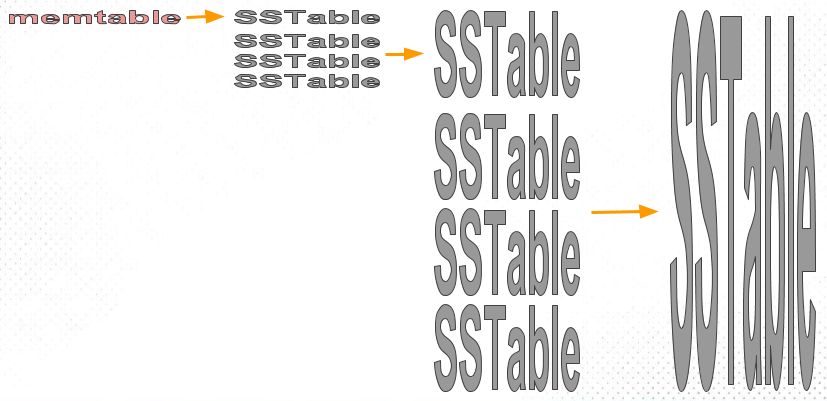
这个算法的弊端在于,大量 SSTable 被创建,且越往下层的 SSTable 体积越大,呈「倒漏斗」形。从概率上分析,越底层的 SSTable 被查询命中的概率越大。在最坏情况下,LSM Tree 的查询会检索全量文件。
level-based 策略则是按分层,而不是按文件大小进行合并。这里也有「层」,但和 size-based 策略区别之处在于:前者是按层的既定大小划分,每层 SSTable 大小差别不大;后者是直接按 SSTable 的大小划分。比如第一层是 300M,第二层是 3G,第三层是 30G,依此类推。参考下图示例。
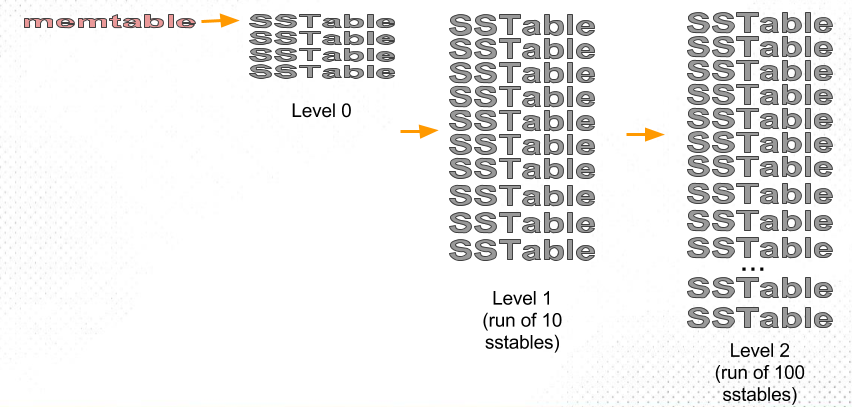
假如 Level K 层大小超过目标大小,则从该层中选择至少一个 SSTable,将该集合和 Level K+1 层有交集的部分合并,生成的新文件写入 K+1 层。如果 K+1 层在接受上一层的合并后又超出了该层大小限制,则继续触发 K+1 层到 K+2 层的合并。下图展示该算法的逻辑:
除了由 MemTable flush 到磁盘生成的 Level 0 层,每层的 SSTable 都是独立排序、互不相交。这样的好处在于检索目标数据时,只需要先定位 SSTable,再二分查找即可,无需检索全部 SSTable。
LSM Tree 的不足和优化
三个放大
存储上有一个 RUM 猜想[7],意思是达到一定阈值后,Read Overhead、Update Overhead、Memory Overhead,系统最多只能满足其中两项,而不能全部满足。这三者之间的权衡引出了三个放大:读放大、写放大、空间放大。
- 读放大:一次查询需要读取的数据页数量,通过加索引可以实现
O(1)、O(logN)的检索,但会写入更多的数据,需要更多的存储空间; - 写放大:物理存储的写入量和逻辑写入量的比值。写放大越大,磁盘 I/O 次数越多;
- 空间放大:存储介质中空间占用和数据库中实际空间的比值。空间放大和冗余数据、临时存储有关;
上文提及 LSM Tree 的两种归并算法,在三个放大上有不同的取舍。
size-based 归并策略中,相邻层的体积比为 N,则「扇出数」等于 N。其归并过程是将当前层 N 个 SSTable 合并成为下一层的 1 个 SSTable,即写放大为 1,但读取的效率相对低,且文件之间有更多的冗余,有更大的读放大和空间放大。
level-based 策略中,「扇出数」也是 N,归并过程中将当前层部分 SSTable 和下一层存在交集的 SSTable 合并,当一个大数据写入时,可能会导致多层同时发生归并,因此它的写放大是比较大的。而另一面,它提高了检索效率、减少了冗余数据,优化了读放大和空间放大。
优化思路
读放大的优化,目的是要减少读取时的磁盘 I/O 次数。前文提到的布隆过滤器可以优化,但只适用于单行点读,对范围读无能为力,还可以使用 Cache 缓存已经被打开的 SSTable 避免磁盘 I/O 读取,比如 LevelDB 使用了 LRUCache。
写放大优化,将 key-value 分开存储,合并重写数据时,只重写 key,而不用重写 value,这样可以大幅减少写入量。但分开存储后,对 key-value 读写需要操作不同文件,特别是在范围读时,会产生多次磁盘随机 I/O。
小结
存储中还有很多有趣的数据结构,都离不开大学计算机课程上最基础的数据结构,再叠加数学思想来适配不同的使用场景。
比如前文提到的 MemTable 比较典型的实现是通过 Skiplist,将简单的链表查找通过区间跳跃优化了查找次数;基于 binlog 进行数据同步时使用的 RingBuffer,本质还是数组。还有图数据库中的图的应用,在涉及类似社交网络等复杂关系运算的领域起到了不可替代的作用。
同时,数据结构在存储之外的方面也有广泛应用,但其思想是通用的。当需要快速索引时,无论是否涉及存储,都可以考虑用树的结构来表达。







